简介
AVL树是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度(都是$O(\log n)$。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。

删除
从AVL树中删除,可以通过把要删除的节点向下旋转成一个叶子节点,接着直接移除这个叶子节点来完成。因为在旋转成叶子节点期间最多有个节点被旋转,而每次AVL旋转耗费固定的时间,所以删除处理在整体上耗费$\mathrm{O}(\log n)$时间。
搜索
可以像普通二叉查找树一样的进行,所以耗费时间$O(\log n)$,因为AVL树总是保持平衡的。不需要特殊的准备,树的结构不会由于查找而改变。
平衡操作
假设平衡因子是左子树的高度减去右子树的高度所得到的值,又假设由于在二叉排序树上插入节点而失去平衡的最小子树根节点的指针为a(即a是离插入点最近,且平衡因子绝对值超过1的祖先节点),则失去平衡后进行的规律可归纳为下列四种情况:
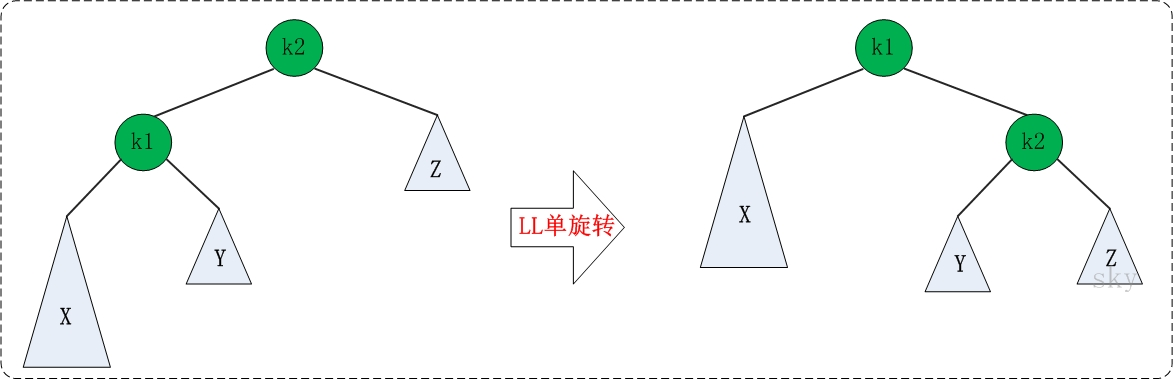
- 单向右旋平衡处理LL:由于在*a的左子树根节点的左子树上插入节点,a的平衡因子由1增至2,致使以a为根的子树失去平衡,则需进行一次右旋转操作;
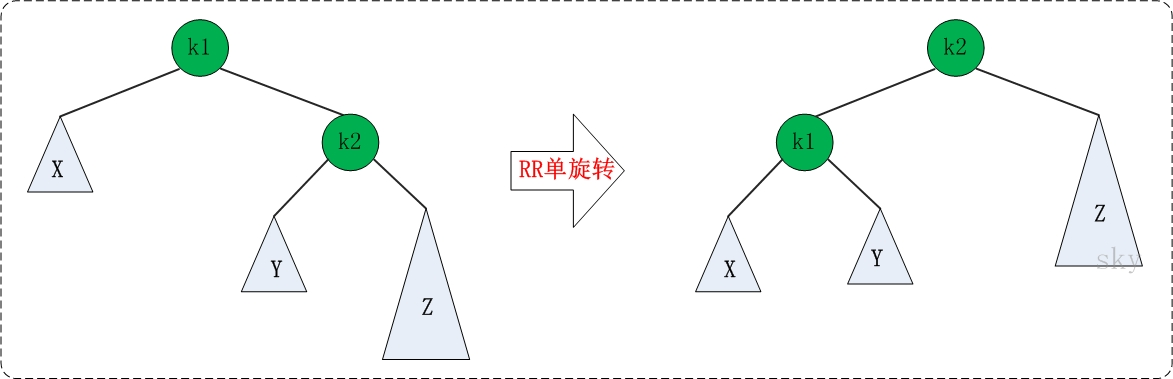
- 单向左旋平衡处理RR:由于在*a的右子树根节点的右子树上插入节点,a的平衡因子由-1变为-2,致使以a为根的子树失去平衡,则需进行一次左旋转操作;
- 双向旋转(先左后右)平衡处理LR:由于在*a的左子树根节点的右子树上插入节点,a的平衡因子由1增至2,致使以a为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
- 双向旋转(先右后左)平衡处理RL:由于在*a的右子树根节点的左子树上插入节点,a的平衡因子由-1变为-2,致使以a为根的子树失去平衡,则需进行两次旋转(先右旋后左旋)操作。

在平衡的二叉排序树BBST (Balancing Binary Search Tree)上插入一个新的数据元素e的递归算法可描述如下:
- 若BBST为空树,则插入一个数据元素为e的新节点作为BBST的根节点,树的深度增1;
- 若e的关键字和BBST的根节点的关键字相等,则不进行;
- 若e的关键字小于BBST的根节点的关键字,而且在BBST的左子树中不存在和e有相同关键字的节点,则将e插入在BBST的左子树上,并且当插入之后的左子树深度增加(+1)时,分别就下列不同情况处理之:
- BBST的根节点的平衡因子为-1(右子树的深度大于左子树的深度,则将根节点的平衡因子更改为0,BBST的深度不变;
- BBST的根节点的平衡因子为0(左、右子树的深度相等):则将根节点的平衡因子更改为1,BBST的深度增1;
- BBST的根节点的平衡因子为1(左子树的深度大于右子树的深度):则若BBST的左子树根节点的平衡因子为1:则需进行单向右旋平衡处理,并且在右旋处理之后,将根节点和其右子树根节点的平衡因子更改为0,树的深度不变;
- 若e的关键字大于BBST的根节点的关键字,而且在BBST的右子树中不存在和e有相同关键字的节点,则将e插入在BBST的右子树上,并且当插入之后的右子树深度增加(+1)时,分别就不同情况处理之。
Java实现
节点
public class AVLTree<T extends Comparable<T>> {
private AVLTreeNode<T> mRoot; // 根结点
// AVL树的节点(内部类)
class AVLTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值) -->排序使用
int height; // 高度
AVLTreeNode<T> left; // 左孩子
AVLTreeNode<T> right; // 右孩子
public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
}高度
/*
* 获取树的高度
*/
private int height(AVLTreeNode<T> tree) {
if (tree != null)
return tree.height;
return 0;
}
public int height() {
return height(mRoot);
}比较大小
/*
* 比较两个值的大小
*/
private int max(int a, int b) {
return a>b ? a : b;
}旋转
LL的旋转
/*
* LL:左左对应的情况(左单旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
AVLTreeNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = max( height(k2.left), height(k2.right)) + 1;
k1.height = max( height(k1.left), k2.height) + 1;
return k1;
}RR的旋转
/*
* RR:右右对应的情况(右单旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
AVLTreeNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max( height(k1.left), height(k1.right)) + 1;
k2.height = max( height(k2.right), k1.height) + 1;
return k2;
}LR的旋转

/*
* LR:左右对应的情况(左双旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}RL的旋转

/*
* RL:右左对应的情况(右双旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}删除
/*
* 删除结点(z),返回根节点
*
* 参数说明:
* tree AVL树的根结点
* z 待删除的结点
* 返回值:
* 根节点
*/
private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) {
// 根为空 或者 没有要删除的节点,直接返回null。
if (tree==null || z==null)
return null;
int cmp = z.key.compareTo(tree.key);
if (cmp < 0) { // 待删除的节点在"tree的左子树"中
tree.left = remove(tree.left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
AVLTreeNode<T> r = tree.right;
if (height(r.left) > height(r.right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
} else if (cmp > 0) { // 待删除的节点在"tree的右子树"中
tree.right = remove(tree.right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
AVLTreeNode<T> l = tree.left;
if (height(l.right) > height(l.left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
} else { // tree是对应要删除的节点。
// tree的左右孩子都非空
if ((tree.left!=null) && (tree.right!=null)) {
if (height(tree.left) > height(tree.right)) {
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> max = maximum(tree.left);
tree.key = max.key;
tree.left = remove(tree.left, max);
} else {
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> min = maximum(tree.right);
tree.key = min.key;
tree.right = remove(tree.right, min);
}
} else {
AVLTreeNode<T> tmp = tree;
tree = (tree.left!=null) ? tree.left : tree.right;
tmp = null;
}
}
return tree;
}
public void remove(T key) {
AVLTreeNode<T> z;
if ((z = search(mRoot, key)) != null)
mRoot = remove(mRoot, z);
}测试
/**
* Java 语言: AVL树
*
* @author skywang
* @date 2013/11/07
*/
public class AVLTreeTest {
private static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
public static void main(String[] args) {
int i;
AVLTree<Integer> tree = new AVLTree<Integer>();
System.out.printf("== 依次添加: ");
for(i=0; i<arr.length; i++) {
System.out.printf("%d ", arr[i]);
tree.insert(arr[i]);
}
System.out.printf("\n== 前序遍历: ");
tree.preOrder();
System.out.printf("\n== 中序遍历: ");
tree.inOrder();
System.out.printf("\n== 后序遍历: ");
tree.postOrder();
System.out.printf("\n");
System.out.printf("== 高度: %d\n", tree.height());
System.out.printf("== 最小值: %d\n", tree.minimum());
System.out.printf("== 最大值: %d\n", tree.maximum());
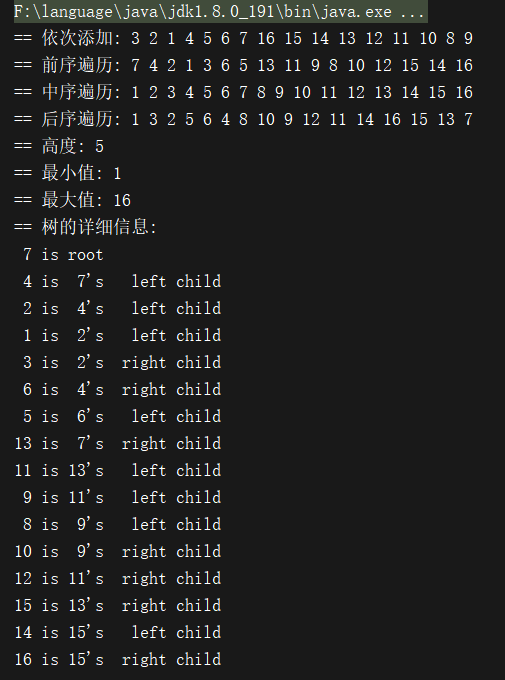
System.out.printf("== 树的详细信息: \n");
tree.print();
i = 8;
System.out.printf("\n== 删除根节点: %d", i);
tree.remove(i);
System.out.printf("\n== 高度: %d", tree.height());
System.out.printf("\n== 中序遍历: ");
tree.inOrder();
System.out.printf("\n== 树的详细信息: \n");
tree.print();
// 销毁二叉树
tree.destroy();
}
}

参考资料
《维基百科》



