Tire
Trie 树,也叫“字典树”,是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。

Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
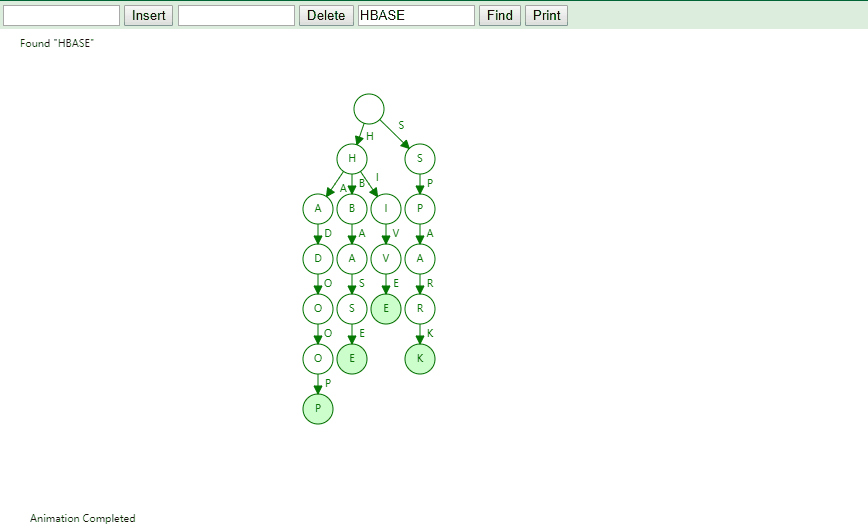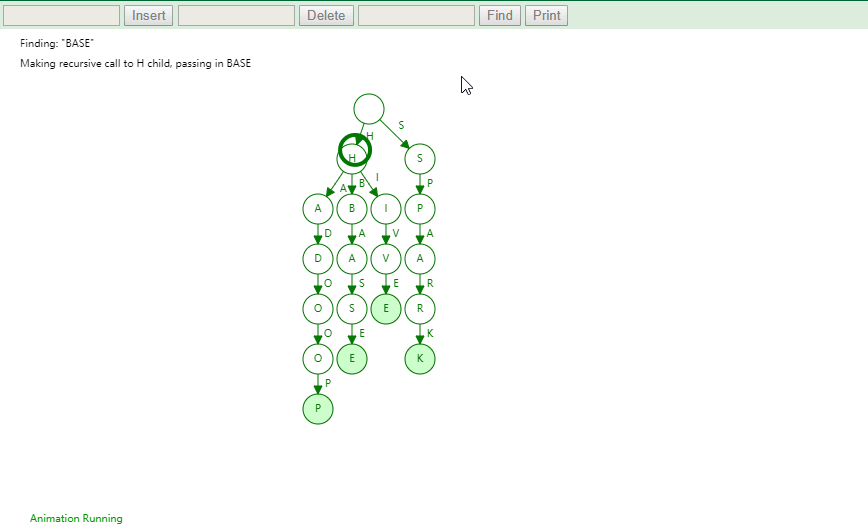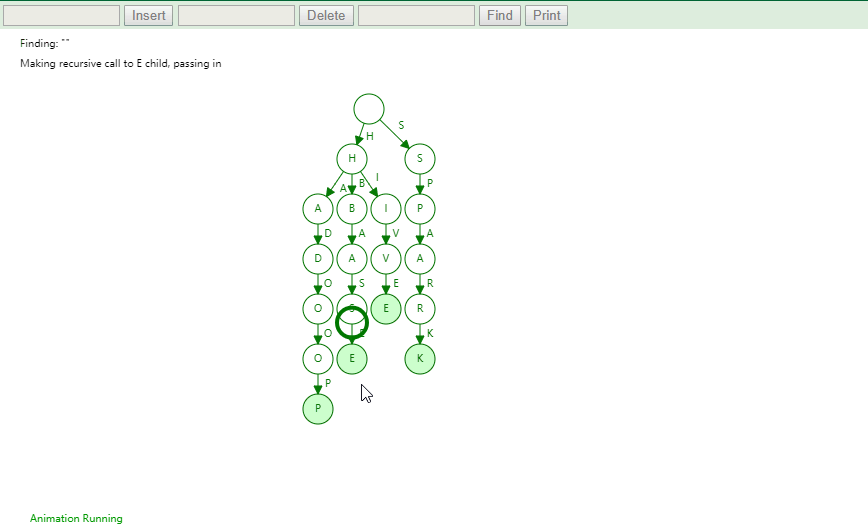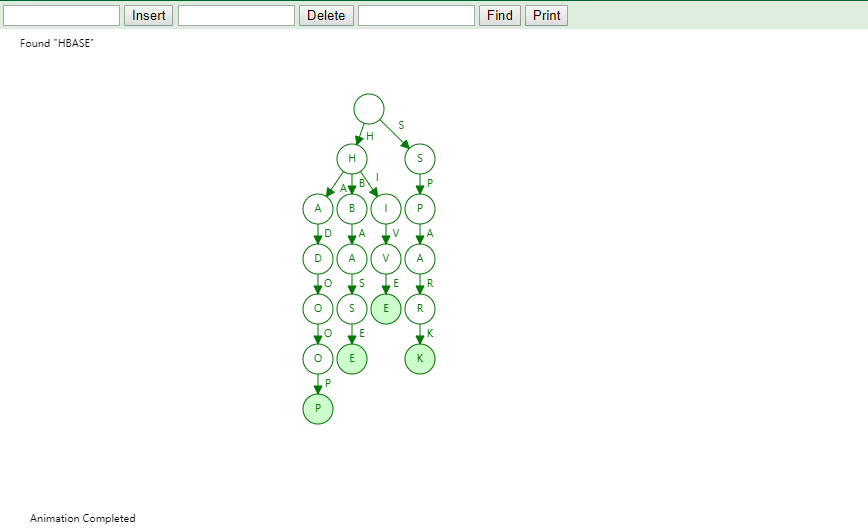
实现
将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
import java.util.HashMap;
public class Trie_Tree{
private class Node{
private int dumpli_num;////该字串的重复数目, 该属性统计重复次数的时候有用,取值为0、1、2、3
private int prefix_num;///以该字串为前缀的字串数, 应该包括该字串本身!!!!!
private Node childs[];////此处用数组实现,当然也可以map或list实现以节省空间
private boolean isLeaf;///是否为单词节点
public Node(){
dumpli_num=0;
prefix_num=0;
isLeaf=false;
childs=new Node[26];
}
}
private Node root;///树根
public Trie_Tree(){
///初始化trie 树
root=new Node();
}
/**
* 插入字串,用循环代替迭代实现
* @param words
*/
public void insert(String words){
insert(this.root, words);
}
/**
* 插入字串,用循环代替迭代实现
* @param root
* @param words
*/
private void insert(Node root,String words){
words=words.toLowerCase();////转化为小写
char[] chrs=words.toCharArray();
for(int i=0,length=chrs.length; i<length; i++){
///用相对于a字母的值作为下标索引,也隐式地记录了该字母的值
int index=chrs[i]-'a';
if(root.childs[index]!=null){
////已经存在了,该子节点prefix_num++
root.childs[index].prefix_num++;
}else{
///如果不存在
root.childs[index]=new Node();
root.childs[index].prefix_num++;
}
///如果到了字串结尾,则做标记
if(i==length-1){
root.childs[index].isLeaf=true;
root.childs[index].dumpli_num++;
}
///root指向子节点,继续处理
root=root.childs[index];
}
}
/**
* 遍历Trie树,查找所有的words以及出现次数
* @return HashMap<String, Integer> map
*/
public HashMap<String,Integer> getAllWords(){
return preTraversal(this.root, "");
}
/**
* 前序遍历。。。
* @param root 子树根节点
* @param prefixs 查询到该节点前所遍历过的前缀
* @return
*/
private HashMap<String,Integer> preTraversal(Node root,String prefixs){
HashMap<String, Integer> map=new HashMap<String, Integer>();
if(root!=null){
if(root.isLeaf==true){
////当前即为一个单词
map.put(prefixs, root.dumpli_num);
}
for(int i=0,length=root.childs.length; i<length;i++){
if(root.childs[i]!=null){
char ch=(char) (i+'a');
////递归调用前序遍历
String tempStr=prefixs+ch;
map.putAll(preTraversal(root.childs[i], tempStr));
}
}
}
return map;
}
/**
* 判断某字串是否在字典树中
* @param word
* @return true if exists ,otherwise false
*/
public boolean isExist(String word){
return search(this.root, word);
}
/**
* 查询某字串是否在字典树中
* @param word
* @return true if exists ,otherwise false
*/
private boolean search(Node root,String word){
char[] chs=word.toLowerCase().toCharArray();
for(int i=0,length=chs.length; i<length;i++){
int index=chs[i]-'a';
if(root.childs[index]==null){
///如果不存在,则查找失败
return false;
}
root=root.childs[index];
}
return true;
}
/**
* 得到以某字串为前缀的字串集,包括字串本身! 类似单词输入法的联想功能
* @param prefix 字串前缀
* @return 字串集以及出现次数,如果不存在则返回null
*/
public HashMap<String, Integer> getWordsForPrefix(String prefix){
return getWordsForPrefix(this.root, prefix);
}
/**
* 得到以某字串为前缀的字串集,包括字串本身!
* @param root
* @param prefix
* @return 字串集以及出现次数
*/
private HashMap<String, Integer> getWordsForPrefix(Node root,String prefix){
HashMap<String, Integer> map=new HashMap<String, Integer>();
char[] chrs=prefix.toLowerCase().toCharArray();
////
for(int i=0, length=chrs.length; i<length; i++){
int index=chrs[i]-'a';
if(root.childs[index]==null){
return null;
}
root=root.childs[index];
}
///结果包括该前缀本身
///此处利用之前的前序搜索方法进行搜索
return preTraversal(root, prefix);
}
}import java.util.HashMap;
public class Trie_Test {
public static void main(String args[]) //Just used for test
{
Trie_Tree trie = new Trie_Tree();
trie.insert("HELLO");
trie.insert("Hadoop");
trie.insert("Hadoop");
trie.insert("Spark");
trie.insert("Flink");
trie.insert("Hbase");
trie.insert("Hive");
trie.insert("Flume");
trie.insert("Kafka");
HashMap<String, Integer> map = trie.getAllWords();
for (String key : map.keySet()) {
System.out.println(key + " 出现: " + map.get(key) + "次");
}
map = trie.getWordsForPrefix("H");
System.out.println("\n\n包含H(包括本身)前缀的单词及出现次数:");
for (String key : map.keySet()) {
System.out.println(key + " 出现: " + map.get(key) + "次");
}
if (trie.isExist("Storm") == false) {
System.out.println("\n\n字典树中不存在:Storm ");
}
}
}



