并查集
在计算机科学中, 并查集是一种树型的数据结构 ,用于处理一些不交集(Disjoint Sets)的合并及查询问题。 有一个联合-查找算法 ( union-find algorithm )定义了两个用于此数据结构的操作:
- Find:确定元素属于哪一个子集。 它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合。
由于支持这两种操作,一个不相交集也常被称为联合-查找数据结构(union-find data structure)或合并-查找集合(merge-find set)。 其他的重要方法,MakeSet,用于建立单元素集合。 有了这些方法,许多经典的划分问题可以被解决。
为了更加精确的定义这些方法,需要定义如何表示集合。 一种常用的策略是为每个集合选定一个固定的元素,称为代表,以表示整个集合。 接着,Find(x) 返回x 所属集合的代表,而Union 使用两个集合的代表作为参数。
UF
public interface UF {
int getSize();
boolean isConnected(int p,int q);
void UnionElements(int p,int q);
}QuickFind
//第一版Union-Find 查询为O(1)级别十分块 缺点:Union的时间复杂度为O(n)
public class UnionFind1 implements UF {
private int[] id;
public UnionFind1(int size) {
id = new int[size];
for (int i = 0; i < id.length; i++) {
id[i] = i;
}
}
@Override
public int getSize() {
return id.length;
}
//查找元素p所对应的集合编号
private int find(int p) {
if (p < 0 && p >= id.length) {
throw new IllegalArgumentException("p is out of bound.");
}
return id[p];
}
//查看元素p和元素q是否属于一个集合
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q是否属于一个集合
@Override
public void UnionElements(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
}
}//第二版Union-Find
public class UniomFind2 implements UF {
private int[] parent;
public UniomFind2(int size) {
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
parent[pRoot] = qRoot;
}
}
QuickUnion
//第二版Union-Find 将每一个元素看作一个节点,节点之间相连接我们看成一个树结构,,孩子指向父亲.通常的实现思路
public class UniomFind2 implements UF {
private int[] parent;
public UniomFind2(int size) {
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
parent[pRoot] = qRoot;
}
}测试
import java.util.Random;
public class Main {
private static double testUF(UF uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.UnionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 100000;
int m = 100000;
UnionFind1 uf1 = new UnionFind1(size);
System.out.println("UnionFind1: " + testUF(uf1, m) + "s");
UniomFind2 uf2 = new UniomFind2(size);
System.out.println("UnionFind2: " + testUF(uf2, m) + "s");
}
}
分析:
UnionFind1整体使用的是一个数组,合并操作,是对连续的内存进行一次循环操作,JVM,对此有很好的优化,对于UnionFind2来说,查询的过程是一个不断索引的过程,不是顺次访问一片连续的内存空间,要在不同的地址之间进行跳转.因此速度会慢一些.在UnionFInd2中Find的时间复杂度为O(h)级别的,操作数越大Union中更多的元素被组织到了一个集合中去.这样树会非常大,
但是又有退化成链表的风险.
Size优化

//第三版Union-Find Size优化 降低树高
public class UniomFind3 implements UF {
private int[] parent;
private int[] sz; //sz[i]表示以i为根的集合中元素个数
public UniomFind3(int size) {
parent = new int[size];
sz = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
sz[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
//根据两个元素所在树的元素个数不同判断合并方向
//将元素个数少的集合合并到元素个数多的集合
if (sz[pRoot] < sz[qRoot]) {
parent[pRoot] = qRoot;
sz[pRoot] += sz[qRoot];
} else {
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
}测试
import java.util.Random;
public class Main {
private static double testUF(UF uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.UnionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 100000;
int m = 100000;
UnionFind1 uf1 = new UnionFind1(size);
System.out.println("UnionFind1: " + testUF(uf1, m) + "s");
UniomFind2 uf2 = new UniomFind2(size);
System.out.println("UnionFind2: " + testUF(uf2, m) + "s");
UniomFind3 uf3 = new UniomFind3(size);
System.out.println("UnionFind3: " + testUF(uf3, m) + "s");
}
}

分析:
在UnionFInd3中,我们可以确保树的深度是十分浅的,虽然时间复杂度为O(h)但是h很小因此,效率会很高.对于UnionFind2来说,在极端情况下,会退化成一个链表.
Rank优化
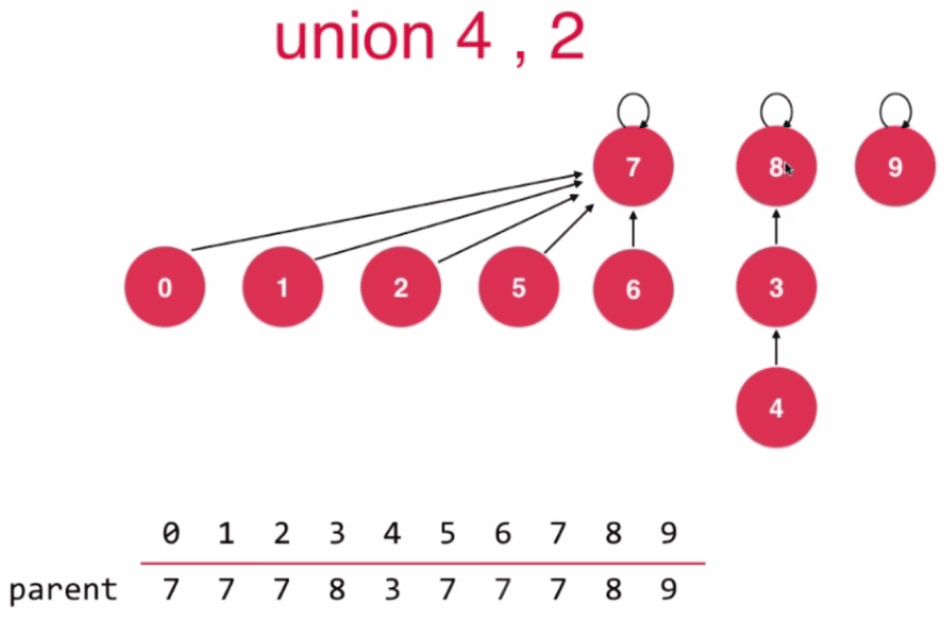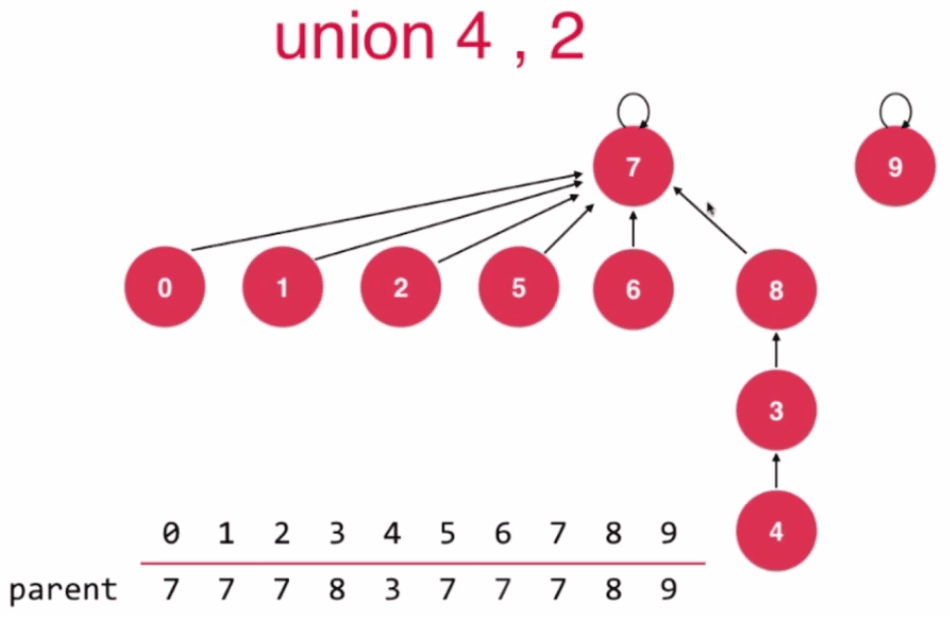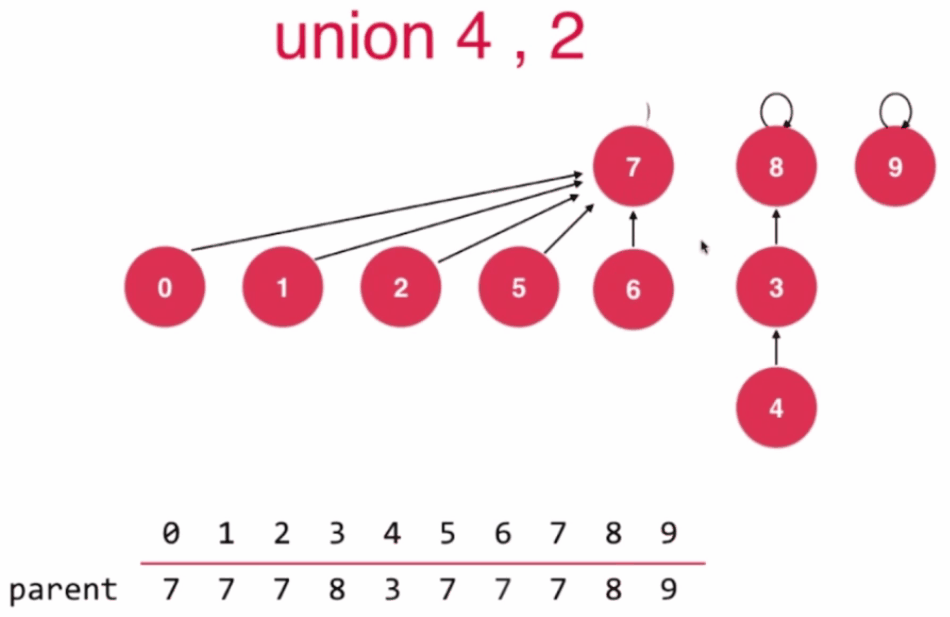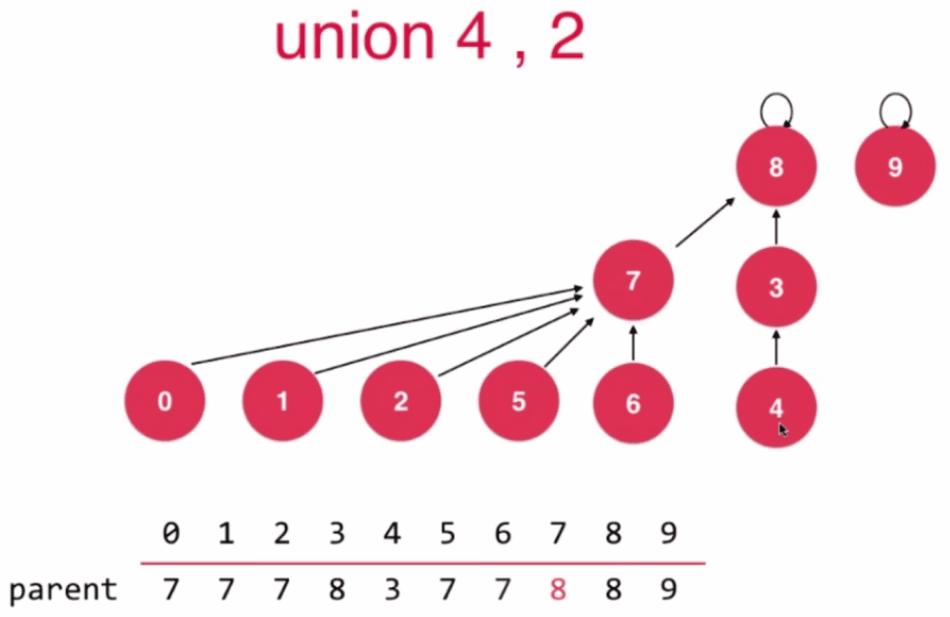
//第四版Union-Find 基于Rank优化
public class UniomFind4 implements UF {
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合所表示的树的层数
public UniomFind4(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
//根据两个元素所在树的rank不同判断合并方向
//rank低的集合合并到rank高的集合上
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
//qRoot的树高没有发生变化
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else { //rank[qRoot] == rank[pRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}测试
import java.util.Random;
public class Main {
private static double testUF(UF uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.UnionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 10000000;
int m = 10000000;
UniomFind3 uf3 = new UniomFind3(size);
System.out.println("UnionFind3: " + testUF(uf3, m) + "s");
UniomFind4 uf4 = new UniomFind4(size);
System.out.println("UnionFind4: " + testUF(uf4, m) + "s");
}
}

对于千万级别的数据的,由于实现并查集的时候,基于Rank的要比基于Size逻辑上更加合理,因此我们大多情况下实现一个并查集是基于Rank实现的.
路径压缩

//第五版Union-Find 路径压缩
public class UniomFind5 implements UF {
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合所表示的树的层数
public UniomFind5(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
//根据两个元素所在树的rank不同判断合并方向
//rank低的集合合并到rank高的集合上
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
//qRoot的树高没有发生变化
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else { //rank[qRoot] == rank[pRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}测试
import java.util.Random;
public class Main {
private static double testUF(UF uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.UnionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 10000000;
int m = 10000000;
UniomFind3 uf3 = new UniomFind3(size);
System.out.println("UnionFind3: " + testUF(uf3, m) + "s");
UniomFind4 uf4 = new UniomFind4(size);
System.out.println("UnionFind4: " + testUF(uf4, m) + "s");
UniomFind5 uf5 = new UniomFind5(size);
System.out.println("UnionFind5: " + testUF(uf5, m) + "s");
}
}

路径压缩[递归]
实际上当我们使用路径压缩的时候,希望路径直接压缩成这个样子的.
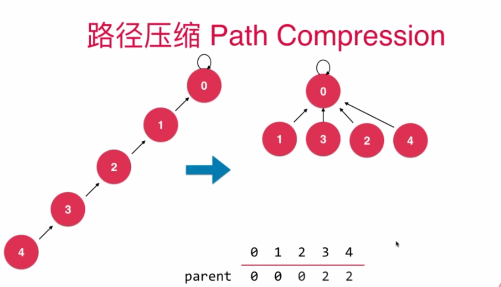
//第六版Union-Find 路径压缩递归实现
public class UniomFind6 implements UF {
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合所表示的树的层数
public UniomFind6(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
//查找过程,查找元素p所对应的集合编号
//O(h)复杂度,h为树的高度
private int find(int p) {
if ((p < 0 && p >= parent.length)) {
throw new IllegalArgumentException("p is out of bound.");
}
while (p != parent[p]) {
parent[p] = find(parent[p]);
p = parent[p];
}
return p;
}
//产看元素是否属于一个集合
//O(h)复杂度,h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
//合并元素p和元素q所属的元素
//O(h)复杂度,h为树的高度
@Override
public void UnionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
//根据两个元素所在树的rank不同判断合并方向
//rank低的集合合并到rank高的集合上
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
//qRoot的树高没有发生变化
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else { //rank[qRoot] == rank[pRoot]
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}测试
import java.util.Random;
public class Main {
private static double testUF(UF uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.UnionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 10000000;
int m = 10000000;
UniomFind3 uf3 = new UniomFind3(size);
System.out.println("UnionFind3: " + testUF(uf3, m) + "s");
UniomFind4 uf4 = new UniomFind4(size);
System.out.println("UnionFind4: " + testUF(uf4, m) + "s");
UniomFind5 uf5 = new UniomFind5(size);
System.out.println("UnionFind5: " + testUF(uf5, m) + "s");
UniomFind6 uf6 = new UniomFind6(size);
System.out.println("UnionFind6: " + testUF(uf6, m) + "s");
}
}
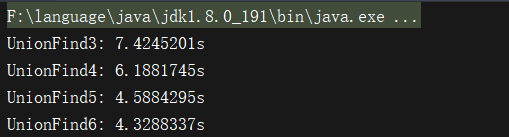
虽然UnionFind6理论上最大压缩了树,但是由于时基于递归实现 虽然会有一丁点的时间消耗但是这次我们测试的数据总量数据千万级别的,因此使用递归实现的压缩,要比非递归实现的要差那么一点点.
并查集时间复杂度

参考资料
《玩转数据结构》



