数据结构之栈 | 菜鸟清风

栈

数据结构

发布日期: 2019-05-03

文章字数: 1.5k

阅读时长: 5 分

阅读次数:

简介

限定仅在表尾进行插入和删除操作的线性表。允许插入和删除的一端成为栈顶，另一端成为栈低，不含任何元素的栈成为空栈，栈又称为先进先出的线性表，简称LIFO结构。

栈的插入操作，叫做进栈，也称压栈，入栈。

栈的删除操作，也叫出战，也有的叫做弹栈。

入栈

出栈

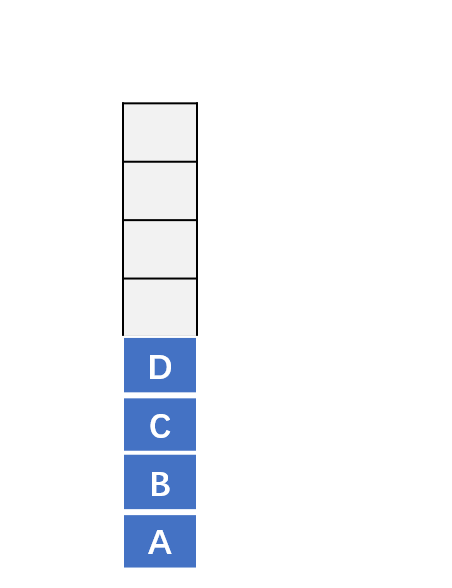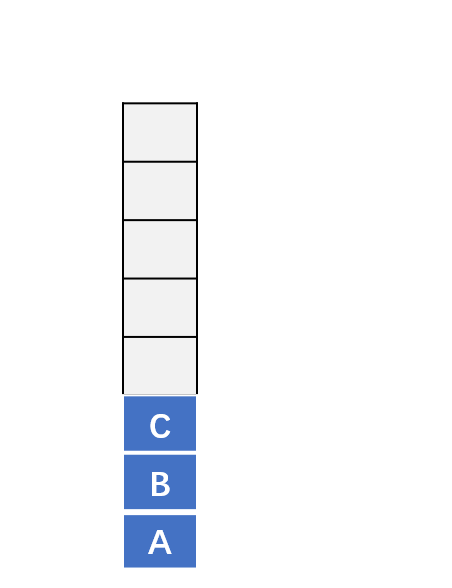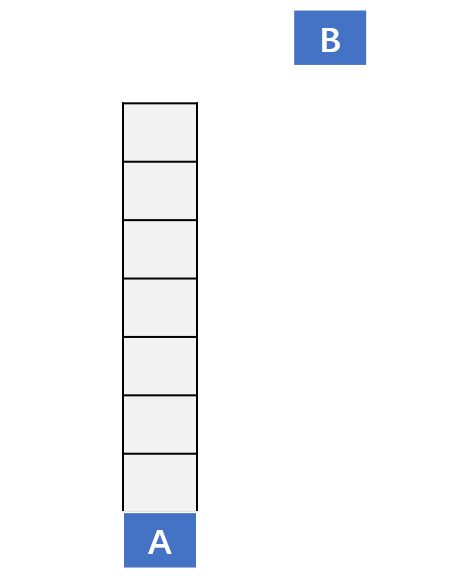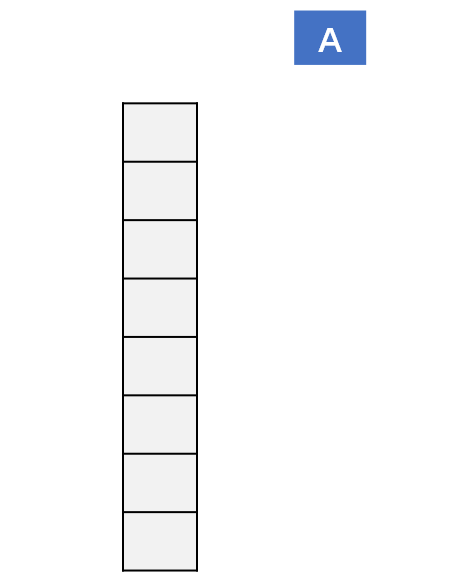
实现一个栈

栈主要包含两个操作，入栈和出栈，也就是在栈顶插入一个数据和从栈顶删除一个数据。栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。
根据上一节我们实现的数组代码我们来实现一个自己的栈。

public interface Stack<E> {

    int getSize();    //获取栈大小
    boolean isEmpty();    //判断是否为空
    void push(E e);        //压栈
    E pop();        //弹栈
    E peek();        //查看栈顶
}

public class ArrayStack<E> implements Stack<E> {

    private Array<E> array;

    public ArrayStack(int capacity){
        array = new Array<>(capacity);
    }

    public ArrayStack(){
        array = new Array<>();
    }

    @Override
    public int getSize(){
        return array.getSize();
    }

    @Override
    public boolean isEmpty(){
        return array.isEmpty();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    public void push(E e){
        array.addLast(e);
    }

    @Override
    public E pop(){
        return array.removeLast();
    }

    @Override
    public E peek(){
        return array.getLast();
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        res.append("Stack: ");
        res.append('[');
        for(int i = 0 ; i < array.getSize() ; i ++){
            res.append(array.get(i));
            if(i != array.getSize() - 1)
                res.append(", ");
        }
        res.append("] top");
        return res.toString();
    }
}

测试

public class Main {

    public static void main(String[] args) {

        ArrayStack<Integer> stack = new ArrayStack<>();

        for(int i = 0 ; i < 6 ; i ++){
            stack.push(i); //压栈
            System.out.println(stack);
        }

        stack.pop(); //弹栈
        System.out.println(stack);
        System.out.println("栈顶为:"+stack.peek());
    }
}

分析

不管是顺序栈还是链式栈，我们存储数据只要一个大小为 n 的数组就够了。入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。
这里存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n)。因为，这 n 个空间是必须的，无法省掉。所以我们说空间复杂度的时候，是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。

出栈的时间复杂度仍然是 O(1)。但是，对于入栈操作来说，情况就不一样。当栈中有空闲空间时，入栈操作的时间复杂度为 O(1)。但当空间不够时，就需要重新申请内存和数据搬移，所以时间复杂度就变成了 O(n)。

摊还分析

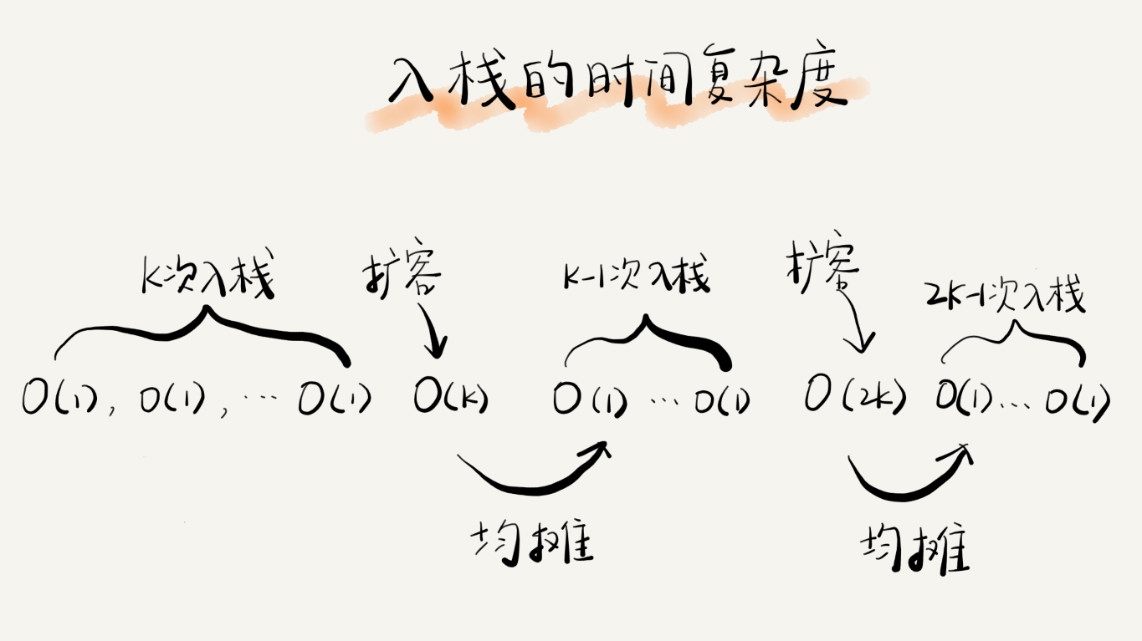
栈空间不够时，我们重新申请一个是原来大小两倍的数组；为了简化分析，假设只有入栈操作没有出栈操作；定义不涉及内存搬移的入栈操作为 simple-push 操作，时间复杂度为 O(1)。如果当前栈大小为 K，并且已满，当再有新的数据要入栈时，就需要重新申请 2 倍大小的内存，并且做 K 个数据的搬移操作，然后再入栈。但是，接下来的 K-1 次入栈操作，我们都不需要再重新申请内存和搬移数据，所以这 K-1 次入栈操作都只需要一个 simple-push 操作就可以完成。

栈应用

函数应用

操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

这是一个比较费流量的GIF！！！

表达式求值

我将算术表达式简化为只包含加减乘除四则运算，比如：34+13*9+44-12/3。对于这个四则运算编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。
如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

在括号匹配

我们假设表达式中只包含三种括号，圆括号 ()、方括号 [] 和花括号{}，并且它们可以任意嵌套。比如，{[{}]}或 [{()}([])] 等都为合法格式，而{[}()] 或 [({)] 为不合法的格式。在给你一个包含三种括号的表达式字符串。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

import java.util.Stack;

class Solution {

    public boolean isValid(String s) {

        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == '(' || c == '[' || c == '{')
                stack.push(c);
            else {
                if (stack.isEmpty())
                    return false;

                char topChar = stack.pop();
                if (c == ')' && topChar != '(')
                    return false;
                if (c == ']' && topChar != '[')
                    return false;
                if (c == '}' && topChar != '{')
                    return false;
            }
        }
        return stack.isEmpty();
    }


    public static void main(String[] args) {

        System.out.println((new Solution()).isValid("({[]})[]{}"));
        System.out.println((new Solution()).isValid("([)]"));
    }
}